测试发布

Hello world!

\begin{cases}
T_2 \cos\alpha_2 - T_1 \cos\alpha_1 = 0 \\ T_2 \sin\alpha_2 - T_1 \sin\alpha_1 = \rho dx \frac{\partial^2 y}{\partial x^2}
\end{cases}

非綫性系統是一門研究人與「家」關係的學問，而非綫性控制則是在探討回家的方法。

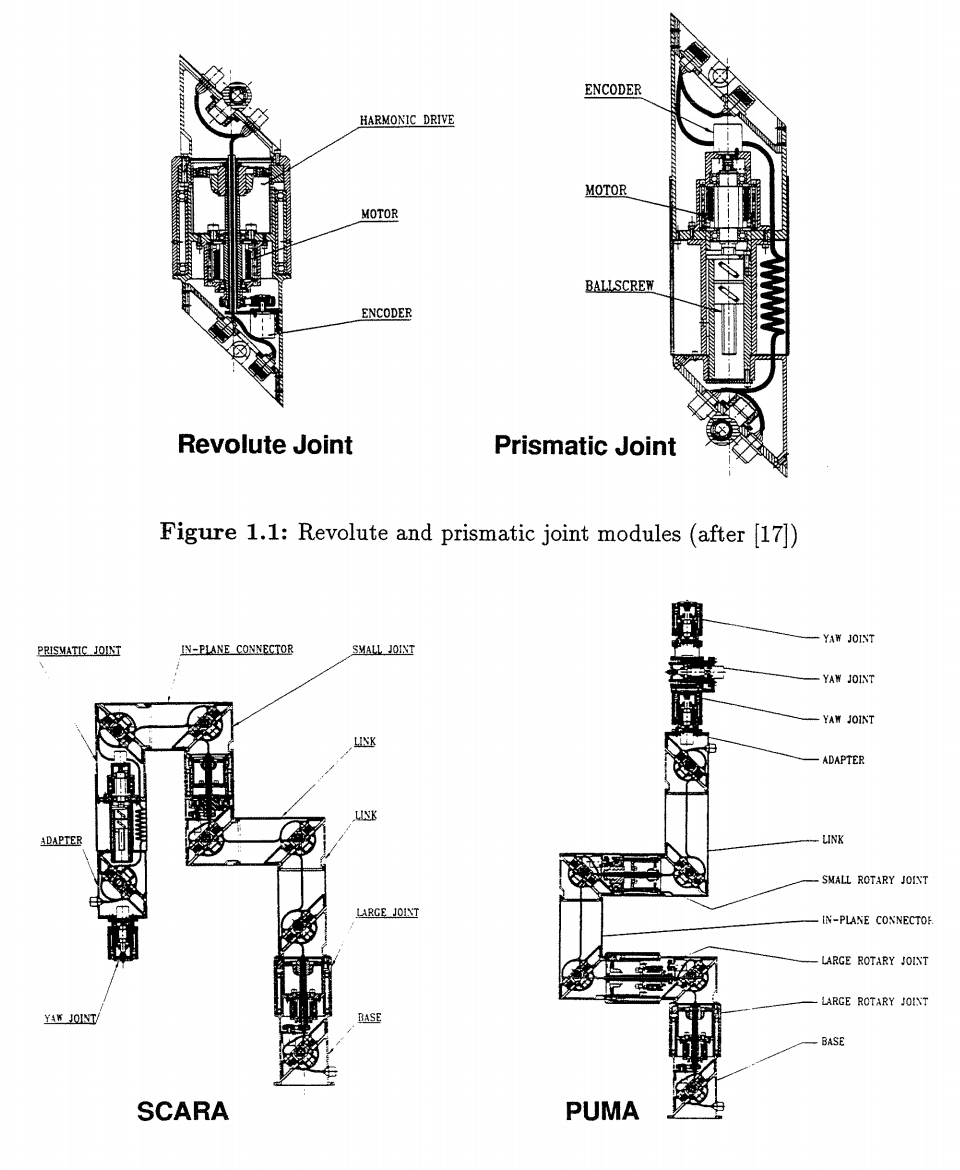
Harmonic-drive transmission:wave generator->flexspline->Circular Spline

Ball-screw transmissio

The connection between modules uses a 45° connecting scheme relative to the module’s main axes.

The first sub-problem is termed module assembly enumeration, which is basically an algebraic problem involving representation of modular robot assembly configurations,equivalence relations, and counting theorems. The solution to this problem was first reported in Chen and Burdick. An explicit expression of the robot assembly configuration using a graph matrix representation termed an assembly incidence matrix(AIM) is defined.This enumeration procedure reduces the complexity and eliminates the generation of a large number of identical assembly configurations by the brute force
enumeration scheme mentioned.

The second sub-problem is termed the task-oriented optimal configurations which is a combinatorial optimization problem.Because modular robots have no predetermined assembly configuration, in order to retain the modularity of the system,an algorithm to automatically generate robot kinematics from an AIM is introduced in advance. Task requirements and kinematic constraints that affect task execution are explicitly formulated in a task-oriented objective function.The domain of this objective function is the set of distinct assembly configurations generated from the enumeration procedure.

The requirement on joint modules

For many robot designs the joint actuators are located close to the base and gear trains or tendons are used to transmit actuator forces. This design strategy reduces the inertia of the entire robot arm. In modular robots, joints have to be self-actuated.

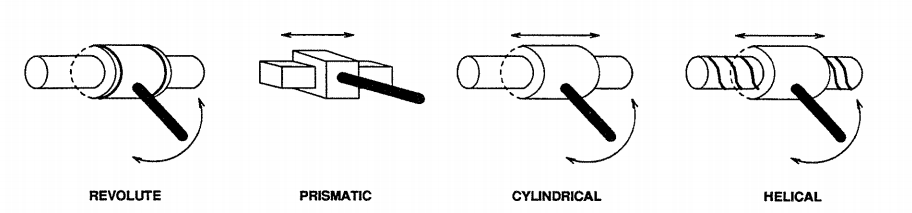
There are six types of joints commonly used, termed “lower pair” joints: Revolute joint(1 DOF), Prismatic joint (1 DOF), Screw joint (1 DOF), Cylindrical joint (2 DOF),Planar joint (2 DOF), and Spherical joint (3 DOF).

The following types of joint modules are assumed to be incorporated in our model modular robotic system:(The notations for joint module types are shown in the parentheses.)

Revolute joint (R): unlimited 1 degree-of-freedom (DOF) rotary motion between two link modules.

Prismatic joint (P):limited 1 DOF translational motion between two links.

Helical joint (H): 1 DOF twisting motion between two links.

Cylindrical joint (C): 2-DOF motion between connected links: one is rotation,the other is translation along the rotation axis.

All joints are connected to link modules through standardized connecting interfaces.